√画像をダウンロード 連立 方程式 解き方 3 つ 196000-連立方程式 解き方 3つ
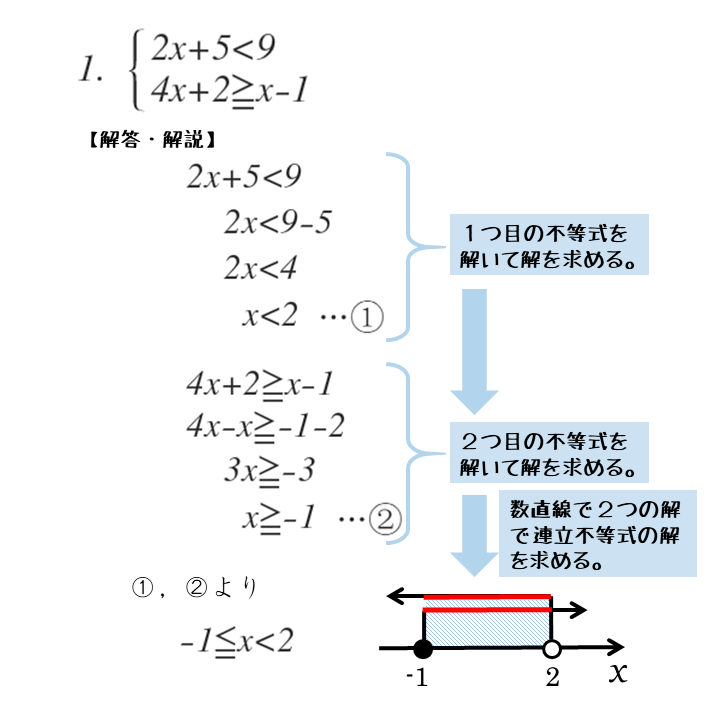
連立方程式の場合、「変数が2つある場合、各変数を1つに定めるためには式が2つなければならない」という特徴がありましたが、連立不等式にはそういった決まりは特にありません。 文字1つに対して、式が3つも4つもある場合があります。 連立不等式の解き方 連立不等式の解き方は通
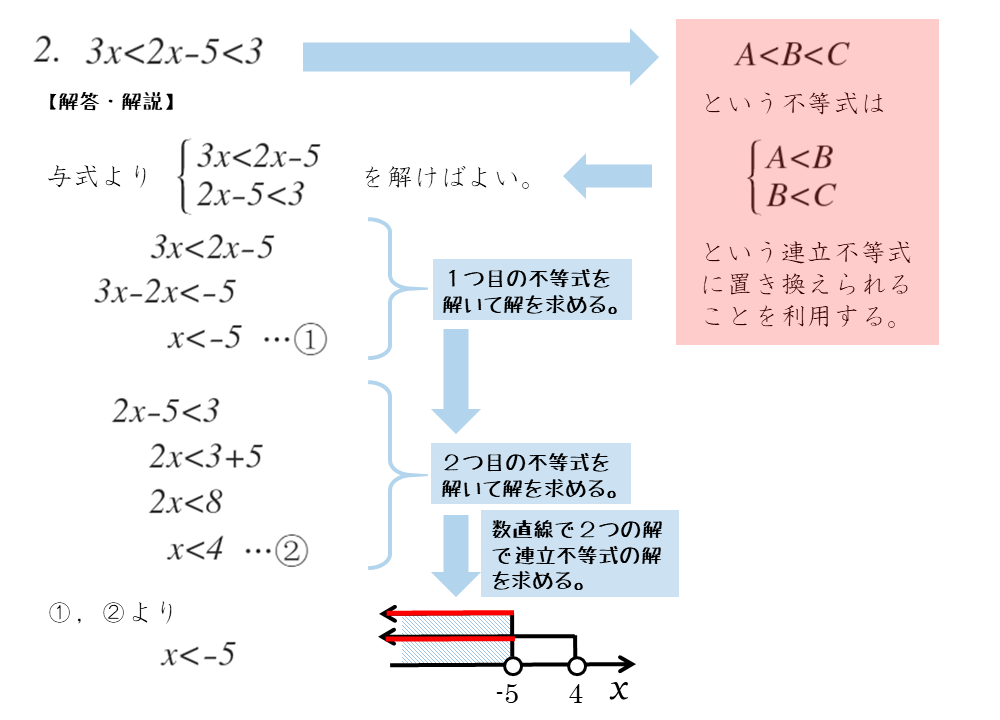
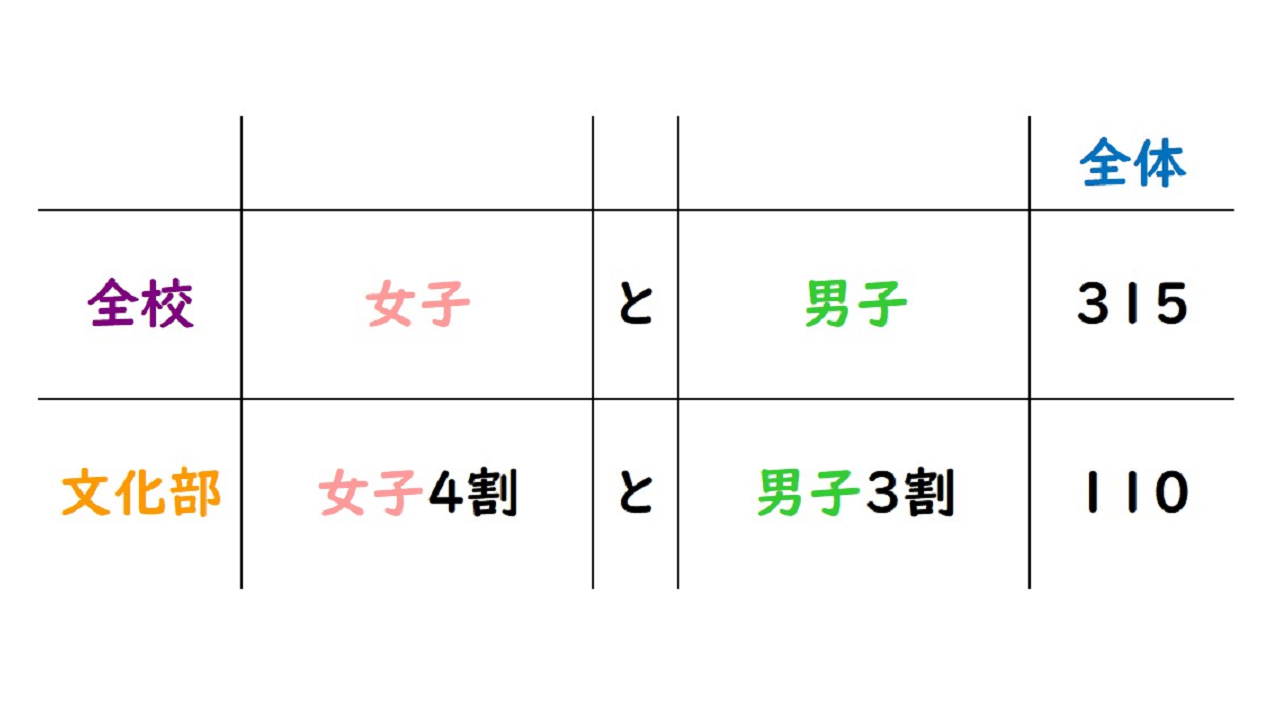
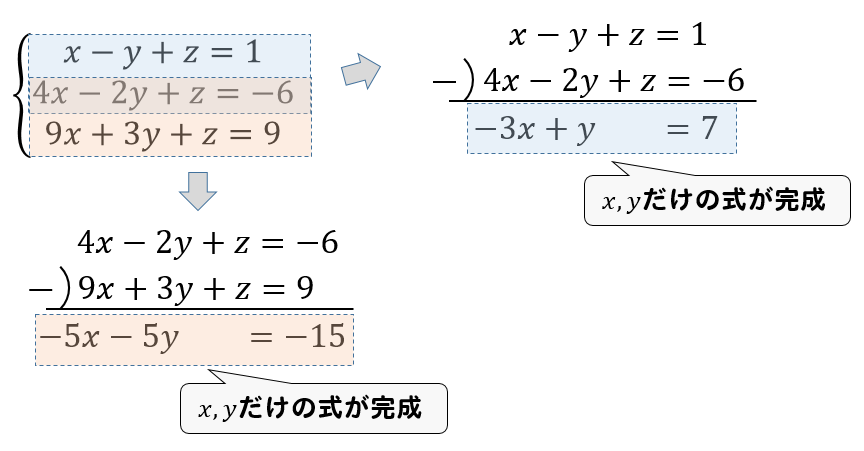
連立方程式 解き方 3つ- 連立方程式「a=b=c」の解き方 次の方程式を解きなさい。 3つの式がつながっているときには、まず3つのうち2つを選んで式を作ります。 さっきとは違うペアでもう1つ式を作ります。 すると、2つ式ができたことになりますね。 ここから連立方程式を作りましょう。 あとは、この連立方程式を解いていけばOKです。 自分で連立方程式を作っちゃえばいんですね連立方程式では,1つの文字を「消去」して文字の個数を減らせばよい. この形の連立方程式では, (1) (2)の y の係数がそろっているところに着目すると, (1) (2)の各辺を「 引き算 」すると y を消去 できます. 例題 C2 次の連立方程式を解きなさい. 3x
連立方程式 解き方 3つのギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | |
 |  | |
 |  |  |
 | ||
「連立方程式 解き方 3つ」の画像ギャラリー、詳細は各画像をクリックしてください。
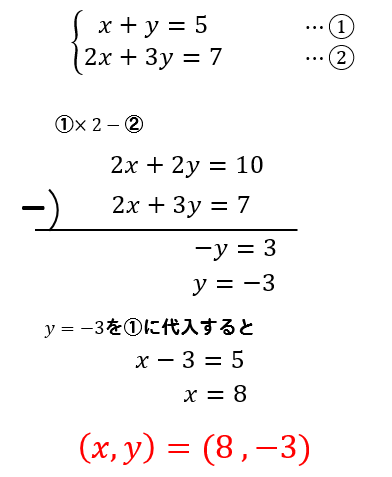 | ||
 |  | |
 |  | |
 |  | |
「連立方程式 解き方 3つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「連立方程式 解き方 3つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
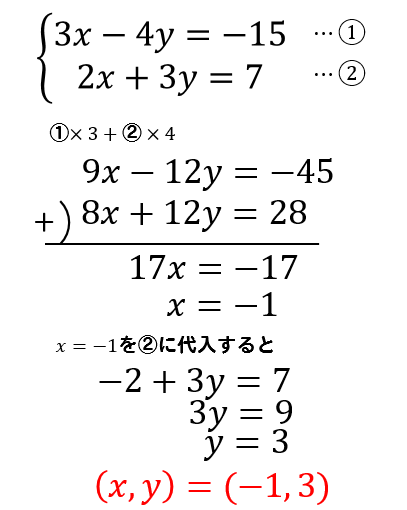 |  |  |
 |  |  |
 |  | |
「連立方程式 解き方 3つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | 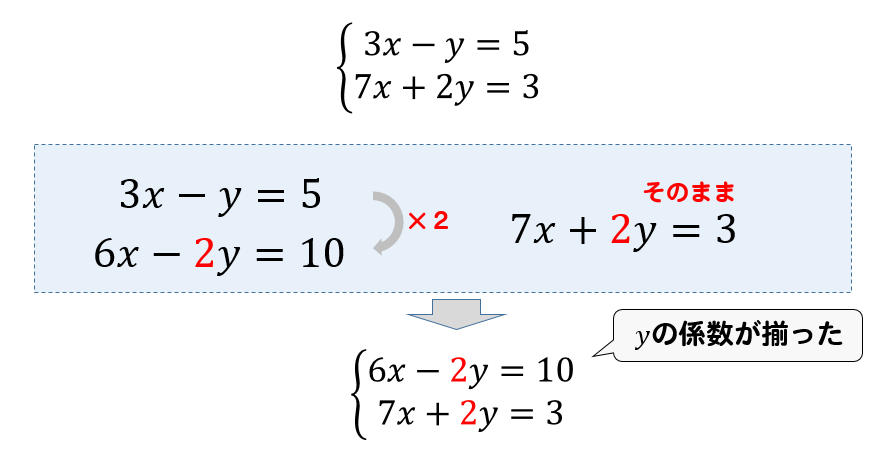 | |
 | 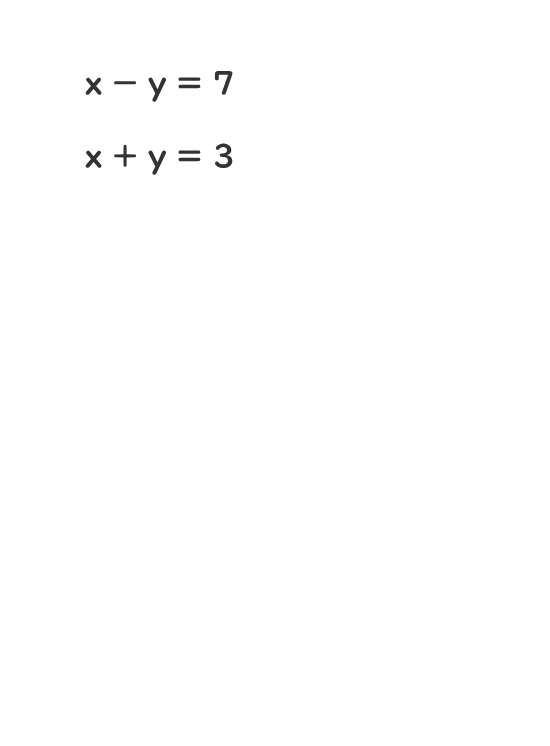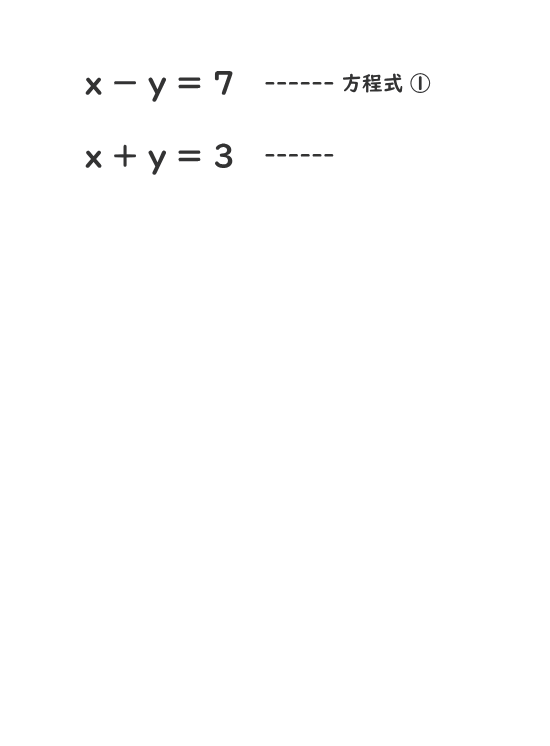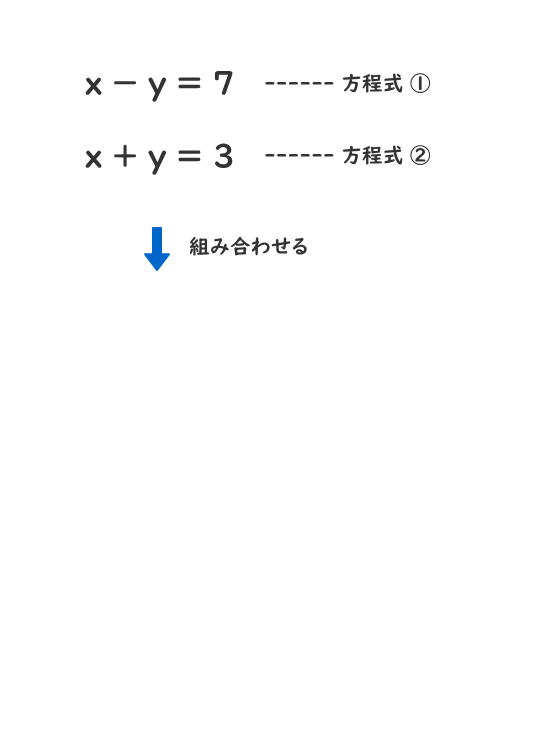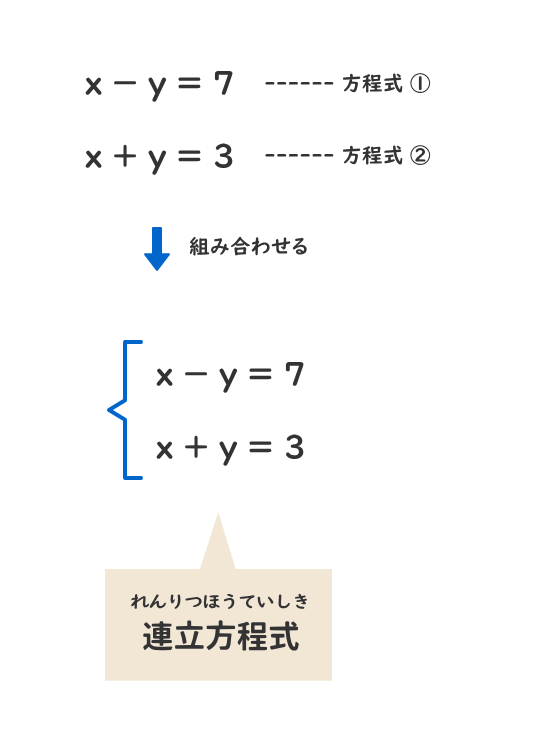 |  |
 |  | |
「連立方程式 解き方 3つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 | ||
 |  |  |
 |  | |
「連立方程式 解き方 3つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | ||
 | 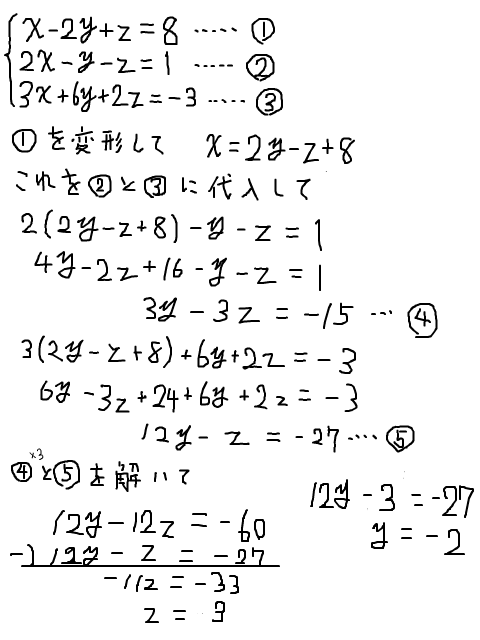 |  |
 |  |  |
「連立方程式 解き方 3つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |  |
 |  |  |
 |  |  |
「連立方程式 解き方 3つ」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 | 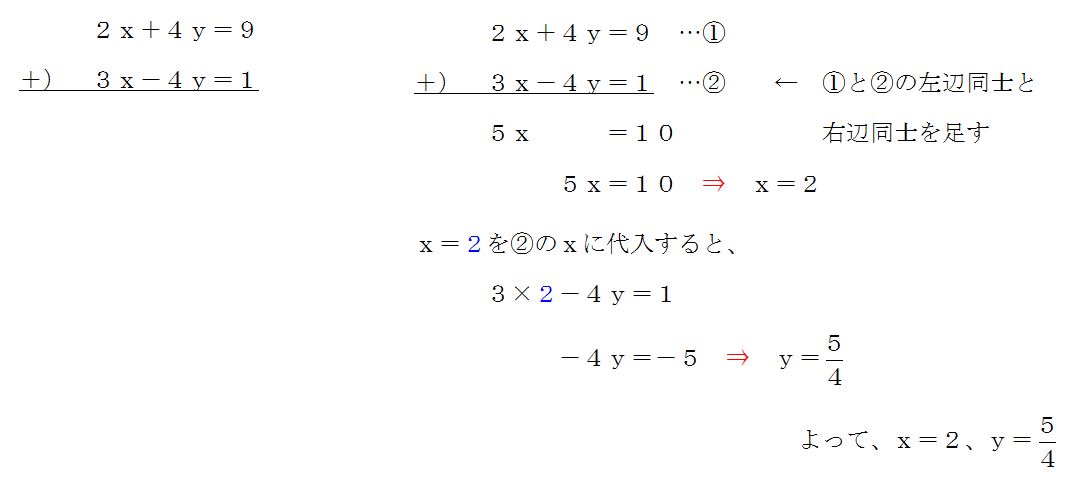 | |
 | 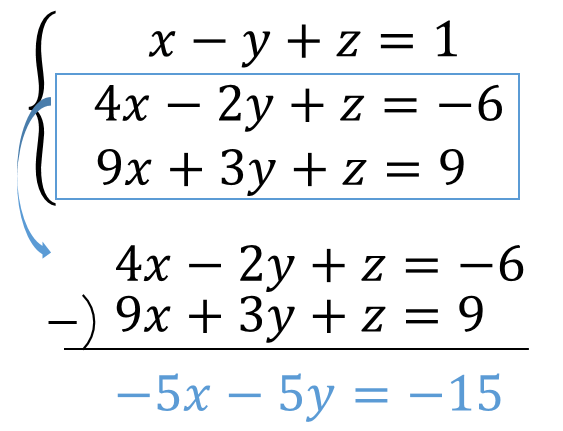 |
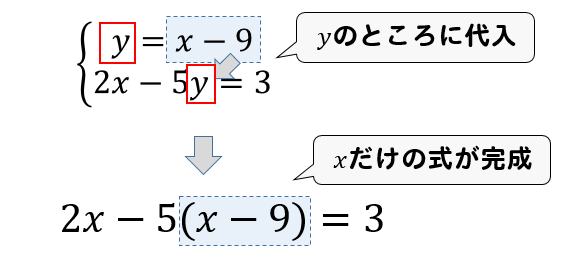
連立方程式の解き方 連立方程式の解き方は、下記の2つがあります。 加減法 ⇒ 1つの未知数が消えるように2つの方程式を加減し、もう一方の未知数の解を求める方法 代入法 ⇒ 1つの式を「x=」の形にして、もう一方の式に代入し解を求める方法連立方程式の解き方は大きく2つあります。それは、 加減法 代入法 です。どちらを用いても解ける問題が大半ですが、それぞれの特徴を抑えつつ、簡単に解説していきます。 加減法を用いた連立方程式
Incoming Term: 連立方程式 解き方 3つ,
コメント
コメントを投稿